Mesh Structure Overview

Table of Contents

• MeshLib Mesh Structure and Topology
  • Mesh
    • Points
    • Topology
  • Mesh Navigation
    • Iterating over valid vertices
    • Iterating over valid faces
    • Iterating ofer vertex edges ring
  • More

MeshLib Mesh Structure and Topology

Mesh

In MeshLib Mesh structure consists of two major parts:

• Points coordinates (Vertices)
• MeshTopology structure
• AABBTree cache (it is used for some algorithms for faster search in mesh, but it does not represent the mesh itself)

Points

Is ordered array of (x,y,z) values for each point (vertex) indexed by VertId (integer value that indicates vertex position in the array)

Topology

Topology in Meshlib is represented as "Half-Edge structure" which means that core primitives are "Half-Edges".
"Half-Edges" are called "Half" because a pair of half edges represent one "Oriented Edge" (one for origin vertex and left face, and the other for destination vertex and right face)
MeshTopology consists of 3 major parts:

• "Half-Edge" records (4 attributes for each "Half-Edge")
• Face to Edge map (for each FaceId stores one EdgeId with this FaceId to the left)
• Vert to Edge map (for each VertId stores one EdgeId with this VertId origin)

Each "Half-Edge" has 4 attributes:

• Origin VertId
• Next "Half-Edge" (to the left, rotating counterclockwise around origin vertex)
• Prev "Half-Edge" (to the right, rotating clockwise around origin vertex)
• Left FaceId

Also there is the opposite "Half-Edge" which can be described as "The Other Half". For example "Oriented Edge" can be considered as a vector from the "Half-Edge" origin vertex to "Other Half" origin vertex.

Each "Half-Edge" is indexed by its unique EdgeId "The Other Half" also have unique EdgeId which is always equal to "Half-Edge" XOR 1

Mesh Navigation

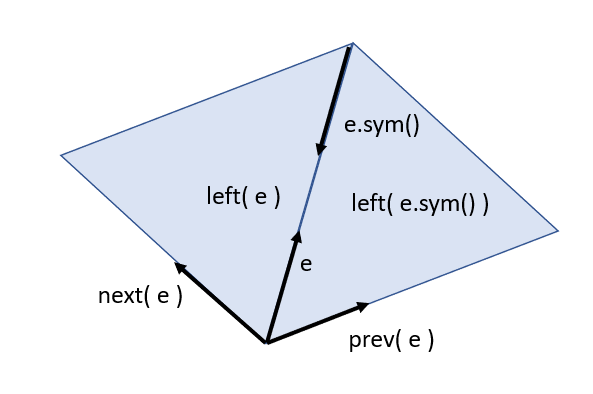
EdgeId e = ... is unique identifier of an oriented edge in mesh ("Half-Edge").

e.sym() - the same edge with opposite orientation ("The Other Half").

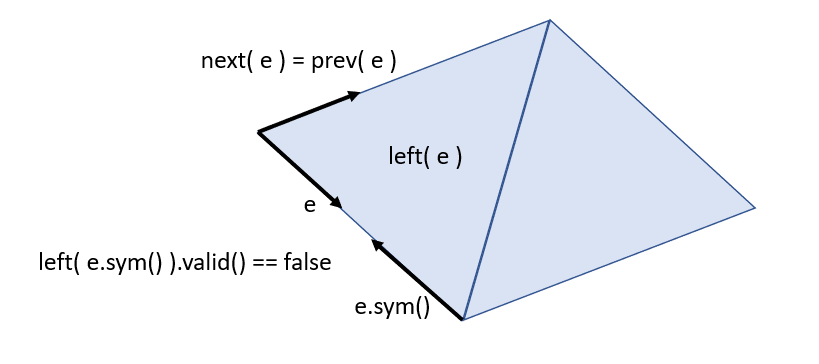
MeshTopology::next( e ) - next in counter-clockwise direction edge from the same origin-ring (Next "Half-Edge").

MeshTopology::prev( e ) - previous in counter-clockwise direction edge from the same origin-ring (Prev "Half-Edge").

MeshTopology::left( e ) - returns the identifier of the face to the left of e. Invalid returned ID means the presence of hole to the left of e (Left FaceId).

MeshTopology::right( e ) - returns the identifier of the face to the right of e. Invalid returned ID means the presence of hole to the right of e (Left FaceId of "The Other Half").

MeshTopology::org( e ) - returns the identifier of the vertex in the origin of e. It is assumed that all edges either have valid vertices on the ends, or "lone" (not connected to the mesh) (Origin VertId).

MeshTopology::dest( e ) - returns the identifier of the vertex in the destination of e. It is assumed that all edges either have valid vertices on the ends, or "lone" (not connected to the mesh) (Origin VertId of "The Other Half").

Iterating over valid vertices

for ( VertId v : mesh.topology.getValidVerts() )
{
    std::cout << mesh.points[v].x << ", " << mesh.points[v].y << ", " << mesh.points[v].z << "\n";
    //...
}

Iterating over valid faces

for ( FaceId f : mesh.topology.getValidFaces() )
{
    ThreeVertIds vertIds;
    mesh.topology.getTriVerts( f, vertIds )
    std::cout << vertIds[0] << ", " << vertIds[1] << ", " << vertIds[2] << "\n";
    //...
}

Iterating ofer vertex edges ring

for ( EdgeId e : orgRing( mesh.topology, vertId ) )
{
    //...
}

Find more advanced mesh navigation techniques in this discussion

More

In general any closed loop of edges may have a single face, but in meshlib we fully support only triangular faces which means that all faces can have strictly 3 edges and 3 vertices incident to it (Mesh structure allows having non-triangular faces but not all algorithms can work with it).

In this paper one can find commonly used mesh structures including "Half-Edge" structure on 18th slide.

In this paper, one can find description of more advanced "Quad-Edge" structure, please find some basic edge functions mapping bellow:

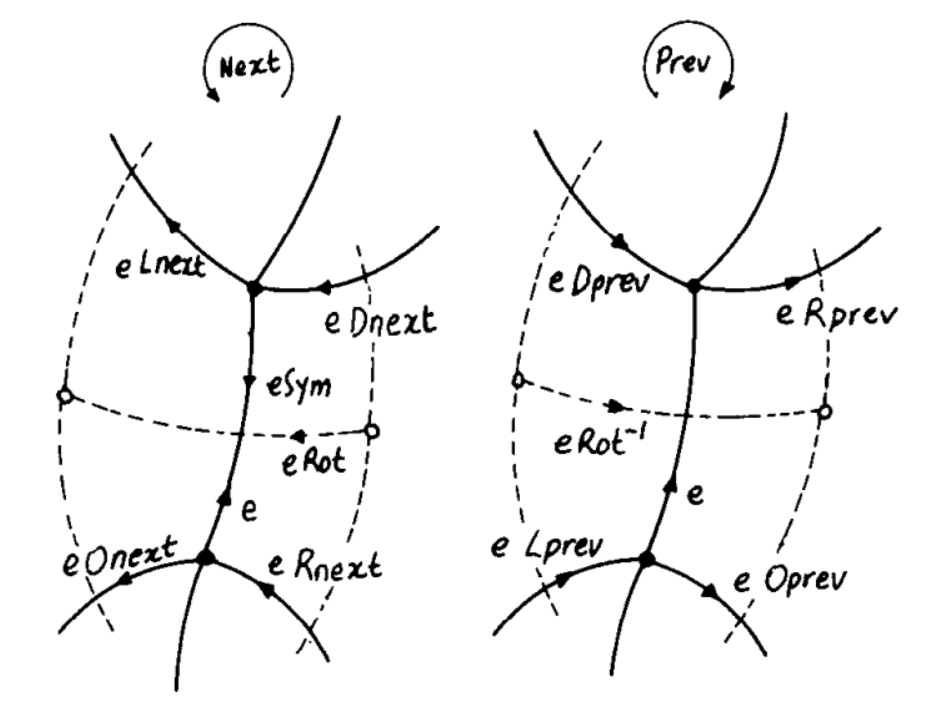
Quad-Edge paper	MeshLib
eSym	e.sym()
eOnext	topology.next(e)
eOprev	topology.prev(e)
eDnext	topology.next(e.sym()).sym()
eDprev	topology.prev(e.sym()).sym()
eLnext	topology.prev( mE.sym() )
eLprev	topology.next( mE ).sym()
eRnext	topology.prev( mE ).sym()
eRprev	topology.next( mE.sym() )