What is Mesh Boolean?

The term ‘Mesh Boolean operations’ refers to a particular set of manipulations that professionals apply to pairs of versatile 3D objects for the purpose of reshaping their geometries. There are several types of them in existence, defined by how exactly their parts ‘interact’ in practice.

The major ones could be boiled down to the following four:

Difference (A-B, aka A AND (NOT B));
Union (‘A+B’ aka OR);
Intersection (A∩B’ aka AND);
Symmetrical difference (‘A^B’ aka XOR).

In the domain of 3D modeling, these constitute the foundation for countless vital workflows. Through them, one is in the perfect position to swiftly create complex shapes based on two initial constituents.

3D Mesh Boolean Types

Input

To illustrate the various mesh Boolean operations, we will use two spheres, Mesh A and Mesh B, as the source shapes for the following examples, which are arranged so they partially overlap. This configuration provides a clear illustration of how each operation transforms the resulting geometry.

Difference

What is the Mesh Boolean Difference method for meshes:

Difference, as its very name implies, subtracts one 3D model from another. There are two options you can try in this context. Either ‘Difference A-B,’ which removes from model A any zone that lies inside model B, or ‘Difference B-A.’ This removes from model B anything what intersects with model A.

Applications:

This technique is widely used in engineering and manufacturing to generate accurate cutouts, cavities, and negative spaces fast. As such, it enables one to design components that fit together seamlessly—e.g., molds, packaging, or custom mechanical parts—by removing intersecting geometries and shaping one object around another.

Synonyms:

A and (NOT B), Subtraction, Cut Out, Remove Parts

A - B = {x \in ℝ^{3} | x \in A \land x \notin B}

How to use 3D Boolean difference:

				
					import meshlib.mrmeshpy as mrmeshpy

# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)

# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)

# perform Difference (A-B) operation
result = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.DifferenceAB)
if not result.valid():
    print(result.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(result.mesh, "out_boolean.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>

#include <iostream>

int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );

    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );

    // perform Difference (A-B) operation
    MR::BooleanResult result = MR::boolean( sphere1, sphere2, MR::BooleanOperation::DifferenceAB );
    MR::Mesh resultMesh = *result;
    if ( !result.valid() )
        std::cerr << result.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( resultMesh, "out_boolean.stl" );

    return 0;
}

				
					#include <MRMeshC/MRMesh.h>
#include <MRMeshC/MRMakeSphereMesh.h>
#include <MRMeshC/MRVector3.h>
#include <MRMeshC/MRAffineXf.h>
#include <MRMeshC/MRMeshBoolean.h>
#include <MRMeshC/MRMeshSave.h>
#include <MRMeshC/MRString.h>

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main( int argc, char* argv[] )
{
    int rc = EXIT_FAILURE;

    // error messages will be stored here
    MRString* errorString = NULL;

    // create first sphere with radius of 1 unit
    MRMakeUVSphereParameters makeParams = mrMakeUvSphereParametersNew();
    makeParams.radius = 1.f;
    makeParams.horizontalResolution = 64;
    makeParams.verticalResolution = 64;
    MRMesh* sphere1 = mrMakeUVSphere( &makeParams );

    // create second sphere by cloning the first sphere and moving it in X direction
    MRMesh* sphere2 = mrMeshCopy( sphere1 );
    MRVector3f xfTranslation = mrVector3fDiagonal( 0.f );
    xfTranslation.x = 0.7f;
    MRAffineXf3f xf = mrAffineXf3fTranslation( &xfTranslation );
    mrMeshTransform( sphere2, &xf, NULL );

    // perform Difference (A-B) operation
    MRBooleanParameters params = mrBooleanParametersNew();
    MRBooleanResult result = mrBoolean( sphere1, sphere2, MRBooleanOperationDifferenceAB, &params );
    if ( result.errorString )
    {
        fprintf( stderr, "Failed to perform boolean: %s", mrStringData( result.errorString ) );
        mrStringFree( errorString );
        goto out;
    }

    // save result to STL file
    MRSaveSettings saveSettings = mrSaveSettingsNew();
    mrMeshSaveToAnySupportedFormat( result.mesh, "out_boolean.stl", &saveSettings, &errorString );
    if ( errorString )
    {
        fprintf( stderr, "Failed to save result: %s", mrStringData( errorString ) );
        mrStringFree( errorString );
        goto out_result;
    }

    rc = EXIT_SUCCESS;
out_result:
    mrMeshFree( result.mesh );
out:
    mrMeshFree( sphere2 );
    mrMeshFree( sphere1 );
    return rc;
}

				
					using System.Reflection;
using static MR.DotNet;

public class MeshBooleanExample
{
    public static void Run(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine("Usage: {0} MeshBooleanExample INPUT1 INPUT2", Assembly.GetExecutingAssembly().GetName().Name);
            return;
        }

        try
        {
            // load mesh
            Mesh meshA = MeshLoad.FromAnySupportedFormat(args[1]);
            Mesh meshB = MeshLoad.FromAnySupportedFormat(args[2]);

            // perform Difference (A-B) operation
            var res = Boolean(meshA, meshB, BooleanOperation.DifferenceAB);

            // save result to STL file
            MeshSave.ToAnySupportedFormat(res.mesh, "out_boolean.stl");
        }
        catch (Exception e)
        {
            Console.WriteLine("Error: {0}", e.Message);
        }
    }
}

Union

What does Mesh Boolean Union do:

This one, logically, combines two entire objects into a single unified structure  by uniting their surfaces.

Applications:

In this capacity, this technique is used to unite multiple shapes into a single, unified model, making it easier to manage and work on intricate designs. This is especially useful in architectural and product design. Across these domains, i.e., those where combining intersecting or adjoining parts matters, this method simplifies your structures for visualization, simulation, or manufacturing.

Synonyms:

OR, Unite Objects, Uniting

A + B : = {x \in ℝ^{3} | x \in A \lor x \in B}

How to Boolean union meshes:

				
					import meshlib.mrmeshpy as mrmeshpy

# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)

# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)

# perform Union operation
result = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.Union)
if not result.valid():
    print(result.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(result.mesh, "out_boolean.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>

#include <iostream>

int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );

    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );

    // perform Union operation
    MR::BooleanResult result = MR::boolean( sphere1, sphere2, MR::BooleanOperation::Union );
    MR::Mesh resultMesh = *result;
    if ( !result.valid() )
        std::cerr << result.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( resultMesh, "out_boolean.stl" );

    return 0;
}

				
					#include <MRMeshC/MRMesh.h>
#include <MRMeshC/MRMakeSphereMesh.h>
#include <MRMeshC/MRVector3.h>
#include <MRMeshC/MRAffineXf.h>
#include <MRMeshC/MRMeshBoolean.h>
#include <MRMeshC/MRMeshSave.h>
#include <MRMeshC/MRString.h>

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main( int argc, char* argv[] )
{
    int rc = EXIT_FAILURE;

    // error messages will be stored here
    MRString* errorString = NULL;

    // create first sphere with radius of 1 unit
    MRMakeUVSphereParameters makeParams = mrMakeUvSphereParametersNew();
    makeParams.radius = 1.f;
    makeParams.horizontalResolution = 64;
    makeParams.verticalResolution = 64;
    MRMesh* sphere1 = mrMakeUVSphere( &makeParams );

    // create second sphere by cloning the first sphere and moving it in X direction
    MRMesh* sphere2 = mrMeshCopy( sphere1 );
    MRVector3f xfTranslation = mrVector3fDiagonal( 0.f );
    xfTranslation.x = 0.7f;
    MRAffineXf3f xf = mrAffineXf3fTranslation( &xfTranslation );
    mrMeshTransform( sphere2, &xf, NULL );

    // perform Union operation
    MRBooleanParameters params = mrBooleanParametersNew();
    MRBooleanResult result = mrBoolean( sphere1, sphere2, MRBooleanOperationUnion, &params );
    if ( result.errorString )
    {
        fprintf( stderr, "Failed to perform boolean: %s", mrStringData( result.errorString ) );
        mrStringFree( errorString );
        goto out;
    }

    // save result to STL file
    MRSaveSettings saveSettings = mrSaveSettingsNew();
    mrMeshSaveToAnySupportedFormat( result.mesh, "out_boolean.stl", &saveSettings, &errorString );
    if ( errorString )
    {
        fprintf( stderr, "Failed to save result: %s", mrStringData( errorString ) );
        mrStringFree( errorString );
        goto out_result;
    }

    rc = EXIT_SUCCESS;
out_result:
    mrMeshFree( result.mesh );
out:
    mrMeshFree( sphere2 );
    mrMeshFree( sphere1 );
    return rc;
}

				
					using System.Reflection;
using static MR.DotNet;

public class MeshBooleanExample
{
    public static void Run(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine("Usage: {0} MeshBooleanExample INPUT1 INPUT2", Assembly.GetExecutingAssembly().GetName().Name);
            return;
        }

        try
        {
            // load mesh
            Mesh meshA = MeshLoad.FromAnySupportedFormat(args[1]);
            Mesh meshB = MeshLoad.FromAnySupportedFormat(args[2]);

            // perform Union operation
            var res = Boolean(meshA, meshB, BooleanOperation.Union);

            // save result to STL file
            MeshSave.ToAnySupportedFormat(res.mesh, "out_boolean.stl");
        }
        catch (Exception e)
        {
            Console.WriteLine("Error: {0}", e.Message);
        }
    }
}

Intersection

What is 3D Boolean Intersection:

When it comes to intersection, its purpose is to generate new objects based on the intersecting portions of two 3D geometries. The resulting intersecting surface can either be used on its own or appended as a Boolean mesh in other activities.

Applications:

Intersection is in demand whenever one needs to assess shared spaces in assembly designs, create cutaway views of sophisticated structures, and accurately model overlapping volumes in mechanical assemblies. The resulting intersecting surface proves itself to be a valuable asset for precision visualization and simulation tasks.

Synonyms:

AND, Common Volume, Overlapping Volume, Mutual Space, Common Area

A \cap B = {x \in ℝ^{3} | x \in A_and_x \in B}

How to use mesh Boolean intersection:

				
					import meshlib.mrmeshpy as mrmeshpy

# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)

# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)

# perform Intersection operation
result = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.Intersection)
if not result.valid():
    print(result.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(result.mesh, "out_boolean.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>

#include <iostream>

int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );

    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );

    // perform Intersection operation
    MR::BooleanResult result = MR::boolean( sphere1, sphere2, MR::BooleanOperation::Intersection );
    MR::Mesh resultMesh = *result;
    if ( !result.valid() )
        std::cerr << result.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( resultMesh, "out_boolean.stl" );

    return 0;
}

				
					#include <MRMeshC/MRMesh.h>
#include <MRMeshC/MRMakeSphereMesh.h>
#include <MRMeshC/MRVector3.h>
#include <MRMeshC/MRAffineXf.h>
#include <MRMeshC/MRMeshBoolean.h>
#include <MRMeshC/MRMeshSave.h>
#include <MRMeshC/MRString.h>

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main( int argc, char* argv[] )
{
    int rc = EXIT_FAILURE;

    // error messages will be stored here
    MRString* errorString = NULL;

    // create first sphere with radius of 1 unit
    MRMakeUVSphereParameters makeParams = mrMakeUvSphereParametersNew();
    makeParams.radius = 1.f;
    makeParams.horizontalResolution = 64;
    makeParams.verticalResolution = 64;
    MRMesh* sphere1 = mrMakeUVSphere( &makeParams );

    // create second sphere by cloning the first sphere and moving it in X direction
    MRMesh* sphere2 = mrMeshCopy( sphere1 );
    MRVector3f xfTranslation = mrVector3fDiagonal( 0.f );
    xfTranslation.x = 0.7f;
    MRAffineXf3f xf = mrAffineXf3fTranslation( &xfTranslation );
    mrMeshTransform( sphere2, &xf, NULL );

    // perform Intersection operation
    MRBooleanParameters params = mrBooleanParametersNew();
    MRBooleanResult result = mrBoolean( sphere1, sphere2, MRBooleanOperationIntersection, &params );
    if ( result.errorString )
    {
        fprintf( stderr, "Failed to perform boolean: %s", mrStringData( result.errorString ) );
        mrStringFree( errorString );
        goto out;
    }

    // save result to STL file
    MRSaveSettings saveSettings = mrSaveSettingsNew();
    mrMeshSaveToAnySupportedFormat( result.mesh, "out_boolean.stl", &saveSettings, &errorString );
    if ( errorString )
    {
        fprintf( stderr, "Failed to save result: %s", mrStringData( errorString ) );
        mrStringFree( errorString );
        goto out_result;
    }

    rc = EXIT_SUCCESS;
out_result:
    mrMeshFree( result.mesh );
out:
    mrMeshFree( sphere2 );
    mrMeshFree( sphere1 );
    return rc;
}

				
					using System.Reflection;
using static MR.DotNet;

public class MeshBooleanExample
{
    public static void Run(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine("Usage: {0} MeshBooleanExample INPUT1 INPUT2", Assembly.GetExecutingAssembly().GetName().Name);
            return;
        }

        try
        {
            // load mesh
            Mesh meshA = MeshLoad.FromAnySupportedFormat(args[1]);
            Mesh meshB = MeshLoad.FromAnySupportedFormat(args[2]);

            // perform Intersection operation
            var res = Boolean(meshA, meshB, BooleanOperation.Intersection);

            // save result to STL file
            MeshSave.ToAnySupportedFormat(res.mesh, "out_boolean.stl");
        }
        catch (Exception e)
        {
            Console.WriteLine("Error: {0}", e.Message);
        }
    }
}

XOR

What is Boolean XOR in 3D:

Regarding symmetrical difference, its task is to generate objects based on the non-intersecting portions. By subtracting the common volume from both sets of triangles, this manipulation leaves behind only the unique parts of each. Such an approach is essential when the eventual priority is to identify and manipulate exclusive design features.

Applications:

Whenever you make Boolean mesh manipulations, symmetrical difference will be your perfect fit for extracting exclusive design elements, performing clash detection, or isolating unique features in hard-to-crack assemblies. The resulting object—being composed of the distinct segments from each of the chosen shapes—will become a valuable asset for targeted analysis and precise simulation tasks.

Synonyms:

XOR, Exclusive OR, Symmetrical Difference, Non-overlapping Volume, Exclusive Area, Complementary Difference

A \oplus B = {x \in ℝ^{3} ∣ (x \in A \land x \notin B) \lor (x \in B \land x \notin A)}

How to use the XOR Boolean operator with 3D mesh (Also note, that it is not 'honest' XOR, as 'honest' XOR would generate non-manifold mesh, which we don’t support):

				
					import meshlib.mrmeshpy as mrmeshpy
 
# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)
 
# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)
 
# perform boolean operations
resultAB = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.DifferenceAB)
resultBA = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.DifferenceBA)
if not resultAB.valid():
    print(resultAB.errorString)
elif not resultBA.valid():
    print(resultBA.errorString)
else:
    # merge BA into AB
    resultAB.mesh.addMesh( resultBA.mesh )
    # save result to STL files
    mrmeshpy.saveMesh(resultAB.mesh, "almost_xor.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>
 
#include <iostream>
 
int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );
 
    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );
 
    // perform a-b boolean operation
    MR::BooleanResult resultAB = MR::boolean( sphere1, sphere2, MR::BooleanOperation::DifferenceAB );
    MR::Mesh abMesh = *resultAB;
    if ( !resultAB.valid() )
        std::cerr << resultAB.errorString << std::endl;
 
    // perform b-a boolean operation
    MR::BooleanResult resultInner = MR::boolean( sphere1, sphere2, MR::BooleanOperation::DifferenceBA );
    MR::Mesh baMesh = *resultBA;
    if ( !resultBA.valid() )
        std::cerr << resultBA.errorString << std::endl;

    // merge ba into ab
    abMesh.addMesh( baMesh );
    // save result to STL files
    MR::MeshSave::toAnySupportedFormat( abMesh, "almost_xor.stl" );
 
    return 0;
}

Split

Having covered the first four classes, we will explore the remaining,  more scenario-specific ones.

What does a 3D Boolean split do:

The task associated with mesh Boolean Split manipulations is manifold. That is, it divides intersecting 3D geometries into distinct segments. What is important is that it does not discard any portion of the original objects. Quite the contrary, it partitions the input models into three parts (or less):

First, the exclusive region of A.
Second, the common intersecting area.
Third, the exclusive region of B.

In this fashion, any splitting round serves users as a non-destructive technique that preserves the entire volume of both shapes and concurrently delineates their boundaries for further processing.

Applications:

Splitting is your choice when all aspects of the original geometry are to be retained and specific regions for detailed modification or assignments must be obtained. They empower those working on precise editing, targeted simulations, and enhanced visualizations. In this case, such specialists need an opportunity to break down compound assemblies into their respective constituent parts.

Synonyms:

Cut, Object Separation, Fragment

Split (A, B) = {A ∖ B, A \cap B, B ∖ A}

How to Boolean split a mesh:

				
					import meshlib.mrmeshpy as mrmeshpy
 
# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)
 
# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)
 
# perform boolean operations
resultOuter = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.DifferenceAB)
resultInner = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.Intersection)
resultOuterB = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.DifferenceBA)
if not resultOuter.valid():
    print(resultOuter.errorString)
elif not resultInner.valid():
    print(resultInner.errorString)
elif not resultOuterB.valid():
    print(resultOuterB.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(resultOuter.mesh, "split_outer_A.stl")
    mrmeshpy.saveMesh(resultInner.mesh, "split_inner.stl")
    mrmeshpy.saveMesh(resultOuterB.mesh, "split_outer_B.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>
#include <iostream>
 
int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );
 
    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );
 
    // perform outer boolean operation
    MR::BooleanResult resultOuter = MR::boolean( sphere1, sphere2, MR::BooleanOperation::DifferenceAB );
    MR::Mesh outerMesh = *resultOuter;
    if ( !resultOuter.valid() )
        std::cerr << resultOuter.errorString << std::endl;
 
    // perform inner boolean operation
    MR::BooleanResult resultInner = MR::boolean( sphere1, sphere2, MR::BooleanOperation::Intersection );
    MR::Mesh innerMesh = *resultInner;
    if ( !resultInner.valid() )
        std::cerr << resultInner.errorString << std::endl;

    // perform other outer boolean operation
    MR::BooleanResult resultOuterB = MR::boolean( sphere1, sphere2, MR::BooleanOperation::DifferenceBA);
    MR::Mesh outerBMesh = *resultOuterB;
    if ( !resultOuterB.valid() )
        std::cerr << resultOuterB.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( outerMesh, "split_outer_A.stl" );
    MR::MeshSave::toAnySupportedFormat( innerMesh, "split_inner.stl" );
    MR::MeshSave::toAnySupportedFormat( outerBMesh, "split_outer_B.stl" );
    return 0;
}

Inside

What is the Boolean Inside ‘operator’ in 3D modeling:

Effectively, ‘Inside’—as a subtype of Intersection—isolates the portion of one shape that lies within the other one. For instance, given our entities include A and B, ‘Inside A’ extracts the segment of A contained in B and vice versa.

Applications:

’Inside’ plays a major part when it comes to advanced modeling scenarios. For instance, ‘A inside B’ works great in scenarios that mandate isolating only the intersecting volume—e.g., creating custom-fit components in mechanical engineering— by adding mesh with Boolean operations to precisely extract the shared section.

Conversely, ‘B inside A’ executes a similar function. It extracts the part of B that lies within A, a method that is frequently applied in reverse engineering to design parts that seamlessly integrate into larger structures.

Synonyms:

Within, Inner, Contained in, Embedded in, Enclosed by

A inside B = A \cap Int (B) = {x \in ℝ^{3} | x \in A \land x \in Int (B)}

*where S(A) and S(B) stand for the surfaces of A and B respectively

How to apply the inside Boolean operator to 3D mesh processing:

				
					import meshlib.mrmeshpy as mrmeshpy

# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)

# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)

# perform Inside(A) operation
result = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.InsideA)
if not result.valid():
    print(result.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(result.mesh, "out_boolean.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>

#include <iostream>

int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );

    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );

    // perform Inside(A) operation
    MR::BooleanResult result = MR::boolean( sphere1, sphere2, MR::BooleanOperation::InsideA );
    MR::Mesh resultMesh = *result;
    if ( !result.valid() )
        std::cerr << result.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( resultMesh, "out_boolean.stl" );

    return 0;
}

				
					#include <MRMeshC/MRMesh.h>
#include <MRMeshC/MRMakeSphereMesh.h>
#include <MRMeshC/MRVector3.h>
#include <MRMeshC/MRAffineXf.h>
#include <MRMeshC/MRMeshBoolean.h>
#include <MRMeshC/MRMeshSave.h>
#include <MRMeshC/MRString.h>

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main( int argc, char* argv[] )
{
    int rc = EXIT_FAILURE;

    // error messages will be stored here
    MRString* errorString = NULL;

    // create first sphere with radius of 1 unit
    MRMakeUVSphereParameters makeParams = mrMakeUvSphereParametersNew();
    makeParams.radius = 1.f;
    makeParams.horizontalResolution = 64;
    makeParams.verticalResolution = 64;
    MRMesh* sphere1 = mrMakeUVSphere( &makeParams );

    // create second sphere by cloning the first sphere and moving it in X direction
    MRMesh* sphere2 = mrMeshCopy( sphere1 );
    MRVector3f xfTranslation = mrVector3fDiagonal( 0.f );
    xfTranslation.x = 0.7f;
    MRAffineXf3f xf = mrAffineXf3fTranslation( &xfTranslation );
    mrMeshTransform( sphere2, &xf, NULL );

    // perform InsideA operation
    MRBooleanParameters params = mrBooleanParametersNew();
    MRBooleanResult result = mrBoolean( sphere1, sphere2, MRBooleanOperationInsideA, &params );
    if ( result.errorString )
    {
        fprintf( stderr, "Failed to perform boolean: %s", mrStringData( result.errorString ) );
        mrStringFree( errorString );
        goto out;
    }

    // save result to STL file
    MRSaveSettings saveSettings = mrSaveSettingsNew();
    mrMeshSaveToAnySupportedFormat( result.mesh, "out_boolean.stl", &saveSettings, &errorString );
    if ( errorString )
    {
        fprintf( stderr, "Failed to save result: %s", mrStringData( errorString ) );
        mrStringFree( errorString );
        goto out_result;
    }

    rc = EXIT_SUCCESS;
out_result:
    mrMeshFree( result.mesh );
out:
    mrMeshFree( sphere2 );
    mrMeshFree( sphere1 );
    return rc;
}

				
					using System.Reflection;
using static MR.DotNet;

public class MeshBooleanExample
{
    public static void Run(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine("Usage: {0} MeshBooleanExample INPUT1 INPUT2", Assembly.GetExecutingAssembly().GetName().Name);
            return;
        }

        try
        {
            // load mesh
            Mesh meshA = MeshLoad.FromAnySupportedFormat(args[1]);
            Mesh meshB = MeshLoad.FromAnySupportedFormat(args[2]);

            // perform InsideA operation
            var res = Boolean(meshA, meshB, BooleanOperation.InsideA);

            // save result to STL file
            MeshSave.ToAnySupportedFormat(res.mesh, "out_boolean.stl");
        }
        catch (Exception e)
        {
            Console.WriteLine("Error: {0}", e.Message);
        }
    }
}

Outside

What is the Boolean Outside operator in 3D modeling:

‘Outside’ isolates the part of one shape that lies completely outside its counterpart. In other words, ‘Outside A’ extracts the segment of A that is not contained in B. Simultaneously, ‘Outside B’ extracts the portion of B that does not intersect with A. We can say that this manipulation is, for all intents and purposes, a subset of Difference. However, together with ‘Inside,’ we highlight it as a distinct method, since it is extremely convenient-to-use.

Applications:

‘Outside’ is undoubtedly vital in terms of subtractive modeling and design refinement. For instance, ‘Outside A’ is helpful for clearing intersecting volumes when you need to create cavities or channels for extra components. At the same time, ‘Outside B’ assists in shaping parts by removing overlapping regions. Both approaches rely on adding mesh with Boolean operations for the sake of maintaining both clear and precise boundaries in the final design.

Synonyms:

Excluding, External, Non-overlapping, Complement, Subtraction

A outside B = A ∖ Int (B) = A \cap (ℝ^{3} ∖ Int (B)) = {x \in ℝ^{3} ∣ x \in A \land x \notin Int (B)}

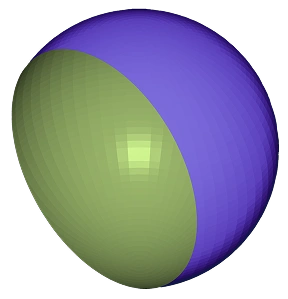
How to apply the outside Boolean operator to 3D mesh processing:

				
					import meshlib.mrmeshpy as mrmeshpy

# create first sphere with radius of 1 unit
sphere1 = mrmeshpy.makeUVSphere(1.0, 64, 64)

# create second sphere by cloning the first sphere and moving it in X direction
sphere2 = mrmeshpy.copyMesh(sphere1)
xf = mrmeshpy.AffineXf3f.translation(mrmeshpy.Vector3f(0.7, 0.0, 0.0))
sphere2.transform(xf)

# perform Outside(A) operation
result = mrmeshpy.boolean(sphere1, sphere2, mrmeshpy.BooleanOperation.OutsideA)
if not result.valid():
    print(result.errorString)
else:
    # save result to STL file
    mrmeshpy.saveMesh(result.mesh, "out_boolean.stl")

				
					#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshBoolean.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRUVSphere.h>

#include <iostream>

int main()
{
    // create first sphere with radius of 1 unit
    MR::Mesh sphere1 = MR::makeUVSphere( 1.0f, 64, 64 );

    // create second sphere by cloning the first sphere and moving it in X direction
    MR::Mesh sphere2 = sphere1;
    MR::AffineXf3f xf = MR::AffineXf3f::translation( MR::Vector3f( 0.7f, 0.0f, 0.0f ) );
    sphere2.transform( xf );

    // perform Outside(A) operation
    MR::BooleanResult result = MR::boolean( sphere1, sphere2, MR::BooleanOperation::OutsideA );
    MR::Mesh resultMesh = *result;
    if ( !result.valid() )
        std::cerr << result.errorString << std::endl;

    // save result to STL file
    MR::MeshSave::toAnySupportedFormat( resultMesh, "out_boolean.stl" );

    return 0;
}

				
					#include <MRMeshC/MRMesh.h>
#include <MRMeshC/MRMakeSphereMesh.h>
#include <MRMeshC/MRVector3.h>
#include <MRMeshC/MRAffineXf.h>
#include <MRMeshC/MRMeshBoolean.h>
#include <MRMeshC/MRMeshSave.h>
#include <MRMeshC/MRString.h>

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main( int argc, char* argv[] )
{
    int rc = EXIT_FAILURE;

    // error messages will be stored here
    MRString* errorString = NULL;

    // create first sphere with radius of 1 unit
    MRMakeUVSphereParameters makeParams = mrMakeUvSphereParametersNew();
    makeParams.radius = 1.f;
    makeParams.horizontalResolution = 64;
    makeParams.verticalResolution = 64;
    MRMesh* sphere1 = mrMakeUVSphere( &makeParams );

    // create second sphere by cloning the first sphere and moving it in X direction
    MRMesh* sphere2 = mrMeshCopy( sphere1 );
    MRVector3f xfTranslation = mrVector3fDiagonal( 0.f );
    xfTranslation.x = 0.7f;
    MRAffineXf3f xf = mrAffineXf3fTranslation( &xfTranslation );
    mrMeshTransform( sphere2, &xf, NULL );

    // perform OutsideA operation
    MRBooleanParameters params = mrBooleanParametersNew();
    MRBooleanResult result = mrBoolean( sphere1, sphere2, MRBooleanOperationOutsideA, &params );
    if ( result.errorString )
    {
        fprintf( stderr, "Failed to perform boolean: %s", mrStringData( result.errorString ) );
        mrStringFree( errorString );
        goto out;
    }

    // save result to STL file
    MRSaveSettings saveSettings = mrSaveSettingsNew();
    mrMeshSaveToAnySupportedFormat( result.mesh, "out_boolean.stl", &saveSettings, &errorString );
    if ( errorString )
    {
        fprintf( stderr, "Failed to save result: %s", mrStringData( errorString ) );
        mrStringFree( errorString );
        goto out_result;
    }

    rc = EXIT_SUCCESS;
out_result:
    mrMeshFree( result.mesh );
out:
    mrMeshFree( sphere2 );
    mrMeshFree( sphere1 );
    return rc;
}

				
					using System.Reflection;
using static MR.DotNet;

public class MeshBooleanExample
{
    public static void Run(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine("Usage: {0} MeshBooleanExample INPUT1 INPUT2", Assembly.GetExecutingAssembly().GetName().Name);
            return;
        }

        try
        {
            // load mesh
            Mesh meshA = MeshLoad.FromAnySupportedFormat(args[1]);
            Mesh meshB = MeshLoad.FromAnySupportedFormat(args[2]);

            // perform OutsideA operation
            var res = Boolean(meshA, meshB, BooleanOperation.OutsideA);

            // save result to STL file
            MeshSave.ToAnySupportedFormat(res.mesh, "out_boolean.stl");
        }
        catch (Exception e)
        {
            Console.WriteLine("Error: {0}", e.Message);
        }
    }
}

Fastest Mesh Boolean Library

As an open source Mesh Boolean library, MeshLib fully enables both rapid and precise manipulation of elaborate geometries. Featuring proprietary advanced algorithms, MeshLib provides developers all over the globe with an opportunity to combine, subtract, or intersect models with swiftly and with ease. In addition to that, we make it possible for developers to repair 3D objects, inspect them, create simple geometries, transform meshes into point clouds, and more.

Whatever your current needs are, being focused on efficiency, our library will also reduce your resource demands.

Finally, in terms of your programming language of choice, MeshLib is built on a powerful C++ core and offers APIs for C, C#, and Python.

How quick are Boolean operations with us:

In case you want to dive deeper into how well-balanced our library is, in terms of speed and quality, check out this practical research.

Key takeaways concerning our performance rates:

Nefertiti Case

Nefertiti mesh, ≈ 2 M triangles

Union

Our result for Union —1.2 s, Intersection—0.7 s, Difference—0.9 s. All outcomes correct

Intersection

Among our contestants, it took the fastest runner‑up 1.3, 1, 1.1  s. to do the job

Difference A-B

As for the rest, it took 3 – 59 s to accomplish the task. Several outcomes were uncorrect.

Dental Case

Dental object, ≈ 0.5 M triangles, noisy data

Union

Our result was 0.18 – 0.20 s for every operation. All outcomes were correct

Intersection

Our closets rival—0.24-0.25 without pre-computing, and 0.47-0.52 with pre-compiting

Difference A-B

With others, it took 0.7 – 15 s. Notably, there were several outright failures

Starting to Work

Now that we have covered the basics and demonstrated our reliability, feel free to follow these instructions to get started with the Mesh Boolean library

Python:

Setup guide
Script writing overview

C++:

Setup guide
Plugin creation guide
MeshLib on GitHub

Download Mesh Boolean Libraries Comparison Results

All benchmark results, including quality comparisons and execution times across all 8 mesh boolean libraries, are available in a downloadable PDF.

To download the full report (PDF),  enter your email

3D Mesh Boolean Algorithms in MeshLib

MeshLib’s 3D Boolean functions harness the Simulation of Simplicity (SoS) framework. Although our algorithm is proprietary, it relies on the principles outlined in this article, which you can explore for more information by clicking on the link.

Long story short, SoS ‘imagines’ that all input data is generic—meaning no perfect coincidences, overlapping edges, or zero distances. As an outcome, this technique operates as though no degenerate situations exist at all. Under the hood, SoS systematically breaks ties and eliminates edge cases, ensuring our algorithms never crash or produce incorrect results when ‘real’ degenerate input data arises.

All in all, the ’Simulation of Simplicity’ principle is a systematic high-performing ‘trick’ that keeps geometry algorithms simpler by pretending everything is just slightly offset from being perfectly aligned.

Getting back to MeshLib:

Our Mesh Boolean algorithms enable all needed activities, including union, intersection, and difference. So you find yourself in the right position to combine, subtract, or intersect problematical geometries with high precision. We also offer extended operations (e.g., isolating parts inside or outside a model), broadening our applicability across various challenges.
MeshLib was crafted with speed in mind. This high efficiency is essential in performance-critical applications like architecture, manufacturing, or aerospace.

Recommended Hardware Configuration for MeshLib

Scenario	Recommended CPU	Recommended GPU
Real-Time Editing	6–8 core CPU with high clock speed	Mid-to-high-end GPU for smooth viewport rendering
Batch Processing (large objects)	12–32 core CPU with high memory bandwidth	Mid-tier GPU, ≥6 GB VRAM
Precision-focused manipulation	High-end CPU with strong double-precision support	GPU not critical. Pro GPU optional for high-fidelity visualization

Success Stories

Here is what our customers say about our efficiency, track record, and usability as a library (including geometry modeling purposes):

Gal Cohen

CTO, customed.ai

“MeshLib has been a game-changer for our company, providing all the essential operations we need to handle meshes and create highly accurate personal surgical instruments (PSIs), which are our primary products. After extensive research and comparison, MeshLib stands out as the best solution on the market. Their team is exceptionally professional and knowledgeable. Collaborating with them has been an absolute pleasure—they respond to any issues we encounter promptly and always deliver effective solutions. Their commitment to customer support and technical excellence is truly unmatched.”

Mariusz Hermansdorfer

Head of Computational Design at Henning Larsen Architechts

“Over the past year, MeshLib has transformed my approach to design and analysis in landscape architecture and architecture projects. This powerful library excels in critical areas, such as geometry processing, interactive booleans, point cloud manipulation, and curve offsetting. These features enhance design workflows, allowing for dynamic modifications, efficient terrain modeling, stormwater flow analysis, and advanced wind flow visualiiza…..”

HeonJae Cho, DDS, MSD, PhD

Chief Executive Officer, 3DONS INC

“MeshLib SDK helped us achieve faster and more accurate calculation results and outperformed any other Mesh Processing library that we evaluated. For us in digital dentistry, it was a game-changer. Mesh processing operations, such as inspecting and editing the mesh to create dental devices for the treatment plan, are crucial. MeshInspector support liberated our team from technical constraints so we concentrated on creating exactly what we wanted. I highly recommend incorporating the MeshLib into your software arsenal.”

Ruedger Rubbert

Chief Technology Officer, Brius Technologies Inc

“With MeshInspector MeshLib we were able to automate many of our workflow processes, thanks to its advanced, modern, and efficient dental and geometry oriented algorithms, covering many of our orthodontic-related tasks: CT and intraoral scan segmentation, voxel and Boolean operations, editing, aligning, visualization, inspection, and import/export of mesh objects. We use the versatile MeshInspector MeshLib API, both in production and R&D for fast prototyping and testing of our ideas.”