What is the 3D Mesh Simplification Method?

Mesh simplification (aka mesh decimation) is, for all intents and purposes, a technique aimed at reducing the number of triangles in 3D models. Concurrently, a properly chosen 3D data processing library will also preserve a decent level of mesh visual quality. Despite its apparent simplicity, this capability is one of the most sought-after ones. Here is why mesh reduction operations are essential.

When dealing with meshes containing thousands—or even millions—of triangles, users:

Might just not require such a high level of resolution and overall visual quality;
May experience unnecessary strain on their respective computational resources.

This is where adequately decimated meshes provide a viable solution. This necessitates simplification.

Types of Mesh Decimation Algorithms in 3D

When it comes to mesh reduction methods, the following approaches are in existence and could be tried, among others:

Edge-collapse. The model progressively simplifies objects by ‘collapsing’ the least-cost edges into single vertices. The classic Quadric Error Metric (QEM) simplification type falls into this category.
Vertex clustering. Your space is partitioned. All vertices within each cell are merged into one. This is a fast and easy-to-implement way. Yet, it could introduce ‘blocky’ artifacts whenever your actual grid is too coarse.
Vertex-removal or point-decimation. Building upon this 3D mesh simplification algorithm, individual vertices get removed according to some cost criterion. The surrounding polygonal hole is re-triangulated. This simplification method tends to preserve overall surface shape but could be slower than edge-collapse.
Multi-resolution encoding. Builds a base, coarse mesh and records a sequence of refinements (vertex splits). You are free to then ‘play back’ fewer splits to get a decimated version.
Simplification envelopes. Two offset surfaces (‘inner’ and ‘outer’) around the original model define a tolerance band. Subsequently, any simplified mesh must stay within these ‘envelopes’. This decimation approach offers acceptable geometric deviation. However, it might be quite complex to compute.
Spectral and wavelet-based methods. These transform the vertex coordinate functions into a spectral domain, discard high-frequency components, and then reconstruct the decimated object.
Curvature-driven decimation. Employs per-vertex curvature estimates to prioritize simplification in ‘flatter’ regions while preserving high-curvature regions. This decimation technique is frequently combined with edge-collapse or vertex-removal to better maintain visual fidelity.

In terms of Python and C++ reduction algorithms, each of the aforementioned simplification methods trades off speed, memory use, and quality, one way or another.

Below, we will explain what you could expect from MeshLib’s C++ and Python simplification (or decimation) algorithm.

How to Simplify a Mesh with MeshLib

MeshLib’s mesh simplification function makes models less detailed by reducing the number of polygons. That happens without noticeably changing how objects look. Here is how it runs. When you call our simplification functionality, you are effectively asking our library to collapse carefully selected edges. The simplification process will stop when a target triangle count or geometric-error threshold is met.

Under the hood, we rely on a QEM edge-collapse queue that evaluates every candidate edge and then removes the one whose collapse introduces the smallest deviation from the original surface.
Boundary edges, creases, per-vertex attributes, and user-defined ‘locked’ regions are honored. Silhouettes and UV/color data survive the operation.
Our decimation function returns a structure that tells you exactly how many faces were removed and how much error was introduced after your simplification round.

In short, ‘decimation’ with us means automated, quality-bounded polygon reduction. It will keep the model visually and topologically faithful, while cutting the associated tech costs.

Users in multiple domains benefit from this simplification potential:

Use case	Why decimate first?
Rendering	Smoother transitions with fewer triangles
Web and mobile delivery	Smaller files stream quickly over constrained networks
Simulation and analysis	Cuts solver time while staying within error tolerances
3D printing and reverse engineering	Trims scanner meshes before slicing or fitting
Digital-twin pipelines	Lightweight meshes that keep positional accuracy

Mesh Simplification: Code Examples in Python and C++

				
					import meshlib.mrmeshpy as mrmeshpy
 
# Load mesh
mesh = mrmeshpy.loadMesh("mesh.stl")
 
# Repack mesh optimally.
# It's not necessary but highly recommended to achieve the best performance in parallel processing
mesh.packOptimally()
 
# Setup decimate parameters
settings = mrmeshpy.DecimateSettings()
 
# Decimation stop thresholds, you may specify one or both
# settings.maxDeletedFaces = 1000 # Number of faces to be deleted
settings.maxError = 0.05 # Maximum error when decimation stops
 
# Number of parts to simultaneous processing, greatly improves performance by cost of minor quality loss.
# Recommended to set to number of CPU cores or more available for the best performance
settings.subdivideParts = 64
 
# Simplify mesh
mrmeshpy.decimateMesh(mesh, settings)
 
# Save result
mrmeshpy.saveMesh(mesh, "decimatedMesh.stl")

				
					#include <MRMesh/MRMeshFwd.h>
#include <MRMesh/MRMeshLoad.h>
#include <MRMesh/MRMeshSave.h>
#include <MRMesh/MRMesh.h>
#include <MRMesh/MRMeshDecimate.h>
#include <MRMesh/MRBuffer.h>

int main()
{
    // Load mesh
    MR::Mesh mesh = *MR::MeshLoad::fromAnySupportedFormat( "mesh.stl" );

    // Repack mesh optimally.
    // It's not necessary but highly recommended to achieve the best performance in parallel processing
    mesh.packOptimally();

    // Setup decimate parameters
    MR::DecimateSettings settings;

    // Decimation stop thresholds, you may specify one or both
    // settings.maxDeletedFaces = 1000; // Number of faces to be deleted
    settings.maxError = 0.05f; // Maximum error when decimation stops

    // Number of parts to simultaneous processing, greatly improves performance by cost of minor quality loss.
    // Recommended to set to the number of available CPU cores or more for the best performance
    settings.subdivideParts = 64;

    // Simplify mesh
    MR::decimateMesh( mesh, settings );

    // Save result
    MR::MeshSave::toAnySupportedFormat( mesh, "decimated_mesh.stl" );

    return 0;
}

Before: almost 414 000 triangles

After: around 84 000 triangles

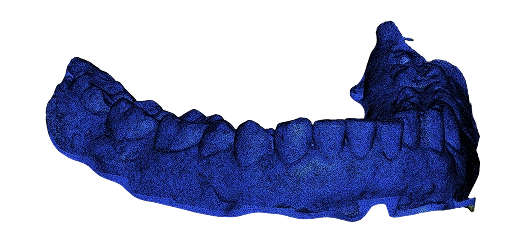
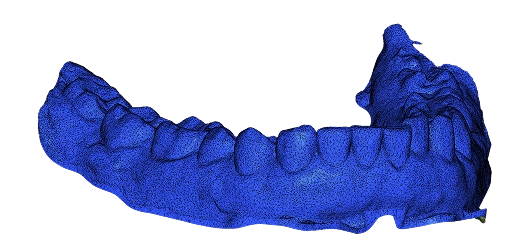
Simplification parameters

Here’s a quick look at how you might fine-tune your mesh decimation flows:

Decide when the simplification should stop. You can limit how much the shape is allowed to change. For that, set a maximum distance deviation from the original mesh. Also, you are free to cap the number of faces or vertices to be deleted. It is also possible to automatically clean up tiny noisy edges by collapsing any edge shorter than a given threshold. Finally, you are in the right position to prevent the creation of overly long edges by setting a maximum allowed edge length.
Keep the quality of the resulting mesh under control. You can limit how stretched the new triangles are allowed to be by setting a maximum aspect ratio. If your original model already has badly shaped faces, you can relax the constraints via a critical aspect ratio setting. If edge flipping is enabled, you could also restrict how much the surface angle is allowed to change by setting a maximum dihedral angle change.
Define which parts of the mesh are allowed to change. You can focus the simplification on a specific region while leaving the rest of the object untouched. Boundary behavior is subject to adjustment too. Control whether collapsing and flipping are allowed near borders. Limit how much boundary vertices are permitted to move, or specify the maximum boundary shift during operations. If needed, you have the leverage to mark particular edges as non-flippable or select exactly which edges are eligible for collapse.
Speed up the simplification process. MeshLib lets you split a mesh into smaller chunks and decimate them in parallel. Before launching parallel decimation, run packOptimally to cluster geometry. After the main decimation round, MeshLib runs a final cleanup pass that now includes the chunk boundaries, so the whole surface reaches a consistent quality level.
Choose your mesh-simplification strategy. By default, MeshLib minimizes geometric deviation by collapsing the edges whose removal alters the shape the least. If you need a more uniform triangulation, choose the “shortest-edge-first” mode instead. This option may introduce slightly more distortion in the final object, but it delivers a regular triangle pattern.
Fine-tune how individual collapses are evaluated. Adjust how geometric deviation is calculated. This becomes possible by enabling angle-weighted measurements or applying a stabilizer to improve results on flat areas. To top it off, one could decide whether vertex positions should be optimized after each collapse to minimize local shape changes.
Customize the process further if needed. MeshLib allows you to plug in your own logic. You can forbid certain collapses and adjust calculated errors. Receive notifications when edges are deleted and track progress during the operation. Advanced users can also preload or capture quadric data. This ensures better control over simplification and synchronizes paired edges across dual meshes.

MeshLib—Open-Source Mesh Simplification Library

MeshLib stands out as the leading choice for mesh simplification. Focusing on our key advantages, here is what can be highlighted:

Outstanding performance. We handle both large and complex objects with increased ease. Up to 10× faster processing speeds is secured, as compared to other solutions. Here, you can find our detailed comparison with VTK, for instance.
Exceptional output quality. Our toolbox maintains high mesh decimation standards. We are fully-equipped to prevent holes, broken surfaces, distorted triangles etc.
Full cross-platform support. Our 3D data processing option runs dependably on Windows, macOS, and Linux. Smooth operation is promised across all major systems.
Modern, future-proof design. Our computational geometry principles are modern. We feature no legacy code that could hold us back.
Flexible and developer-friendly APIs. C++, C#, and Python are on the table. MeshLib makes it straightforward to integrate into diverse software development environments.
Seamless web integration. With WebAssembly supported, high-performance mesh simplification directly inside web browsers becomes possible.

Video Guide: Mesh Simplification with Us

MeshLib is natively developed in C++. Simultaneously, official API bindings for C, C#, and Python are provided:

Python Setup Instructions

C++ Setup Instructions

Version Compatibility Overview:

C++ — Fully supported across all environments.
Python — Compatible with versions 3.8 through 3.13 across major platforms. Please note:
- Windows: Python 3.8–3.13
- macOS: Python 3.8–3.13 (excluding 3.8 on macOS x64)
- Linux: Python 3.8–3.13 on distributions that support manylinux_2_31+

Our mesh simplification library on GitHub for C++ and Python

What our customers say

Gal Cohen

CTO, customed.ai

“MeshLib has been a game-changer for our company, providing all the essential operations we need to handle meshes and create highly accurate personal surgical instruments (PSIs), which are our primary products. After extensive research and comparison, MeshLib stands out as the best solution on the market. Their team is exceptionally professional and knowledgeable. Collaborating with them has been an absolute pleasure—they respond to any issues we encounter promptly and always deliver effective solutions. Their commitment to customer support and technical excellence is truly unmatched.”

Mariusz Hermansdorfer

Head of Computational Design at Henning Larsen Architechts

“Over the past year, MeshLib has transformed my approach to design and analysis in landscape architecture and architecture projects. This powerful library excels in critical areas, such as geometry processing, interactive booleans, point cloud manipulation, and curve offsetting. These features enhance design workflows, allowing for dynamic modifications, efficient terrain modeling, stormwater flow analysis, and advanced wind flow visualiiza…..”

HeonJae Cho, DDS, MSD, PhD

Chief Executive Officer, 3DONS INC

“MeshLib SDK helped us achieve faster and more accurate calculation results and outperformed any other Mesh Processing library that we evaluated. For us in digital dentistry, it was a game-changer. Mesh processing operations, such as inspecting and editing the mesh to create dental devices for the treatment plan, are crucial. MeshInspector support liberated our team from technical constraints so we concentrated on creating exactly what we wanted. I highly recommend incorporating the MeshLib into your software arsenal.”

Ruedger Rubbert

Chief Technology Officer, Brius Technologies Inc

“With MeshInspector MeshLib we were able to automate many of our workflow processes, thanks to its advanced, modern, and efficient dental and geometry oriented algorithms, covering many of our orthodontic-related tasks: CT and intraoral scan segmentation, voxel and Boolean operations, editing, aligning, visualization, inspection, and import/export of mesh objects. We use the versatile MeshInspector MeshLib API, both in production and R&D for fast prototyping and testing of our ideas.”

Start Your Journey with MeshLib

MeshLib SDK offers multiple ways to dive in — from live technical demos to full application trials and hands-on SDK access. No complicated setups or hidden steps. Just the tools you need to start building smarter, faster, and better.

MeshLib Team

Core Developers

MeshLib Team, official authors of MeshInspector App and MeshLib SDK, leverages over 20 years of 3D data-processing and mathematical expertise to deliver high-performance, plug-and-play algorithms that simplify even the most complex mesh workflows.

Leave a review about this post

Share this post on social media